Introduction
Uppaal is an integrated tool environment for modeling, simulation and verification of real-time systems, developed jointly by Basic Research in Computer Science at Aalborg University in Denmark and the Department of Information Technology at Uppsala University in Sweden. It is appropriate for systems that can be modeled as a collection of non-deterministic processes with finite control structure and real-valued clocks, communicating through channels or shared variables [WPD94, LPW97b]. Typical application areas include real-time controllers and communication protocols in particular, those where timing aspects are critical.
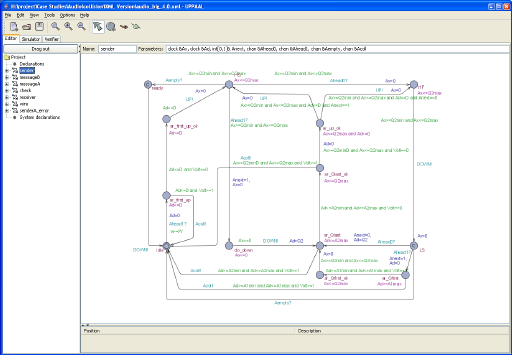
Figure 1: The editor in the Uppaal GUI.
Uppaal consists of three main parts: a description language, a simulator and a model-checker. The description language is a non-deterministic guarded command language with data types (e.g. bounded integers, arrays, etc.). It serves as a modeling or design language to describe system behavior as networks of automata extended with clock and data variables. The simulator is a validation tool which enables examination of possible dynamic executions of a system during early design (or modeling) stages and thus provides an inexpensive mean of fault detection prior to verification by the model-checker which covers the exhaustive dynamic behavior of the system. The model-checker can check invariant and reachability properties by exploring the state-space of a system, i.e. reachability analysis in terms of symbolic states represented by constraints.
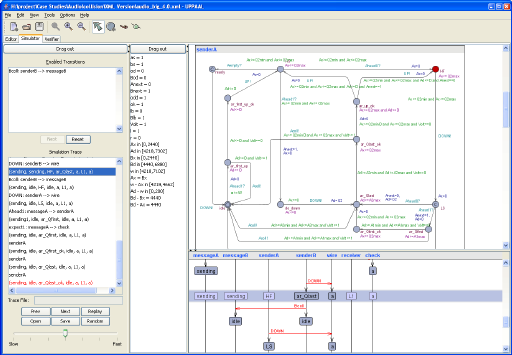
Figure 2: The simulator in the Uppaal GUI. The MSC view in the lower right part is a new feature in Uppaal 3.4.
The two main design criteria for Uppaal have been efficiency and ease of usage. The application of on-the-fly searching technique has been crucial to the efficiency of the Uppaal model-checker. Another important key to efficiency is the application of a symbolic technique that reduces verification problems to that of efficient manipulation and solving of constraints [WPD94, LPW95c, LLPW97, BLPWW99]. To facilitate modeling and debugging, the Uppaal model-checker may automatically generate a diagnostic trace that explains why a property is (or is not) satisfied by a system description. The diagnostic traces generated by the model-checker can be loaded automatically to the simulator, which may be used for visualization and investigation of the trace.
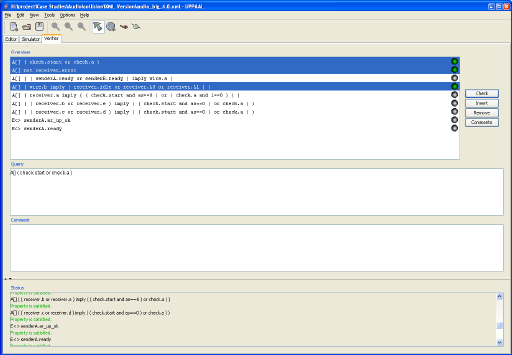
Figure 3: The verifier in the Uppaal GUI.
Since its first release in 1995, Uppaal has been applied in a number of case studies (see Case Studies). To meet requirements arising from the case studies, the tool has been extended with various features. The version Uppaal2k, was first released in September 1999. It is a client/server application implemented in Java and C++, and is currently available for Linux, SunOS and Windows 95/98/NT. The features of Uppaal include:
- A graphical system editor allowing graphical descriptions of systems.
- A graphical simulator which provides graphical visualization and recording of the possible dynamic behaviors of a system description, i.e. sequences of symbolic states of the system. It may also be used to visualize traces generated by the model-checker. Since version 3.4 the simulator can visualize a trace as a message sequence chart (MSC).
- A requirement specification editor that also constitutes a graphical user interface to the verifier of Uppaal2k.
- A model-checker for automatic verification of safety and bonded-liveness properties by reachability analysis of the symbolic state-space. Since version 3.2 it can also check liveness properties.
- Generation of diagnostic traces in case verification of a particular real-time system fails. The diagnostic traces may be automatically loaded and graphically visualized using the simulator. Since version 3.4 it is possible to specify that the generated trace should be the shortest or the fastest.
Statistical Model Checking
What is Statistical Model Checking?
Statistical Model Checking (SMC) refers to a series of techniques that monitor several runs of the system with respect to some property, and then use results from the statistics to get an overall estimate of the correctness of the design. The approach has been applied to problems that are far beyond the scope of existing model checkers. In fact, SMC gets widely accepted in various research areas such as systems biology [JCLLPZ09, CFLHJL08] or software engineering [You05a], in particular for industrial applications [BBBCDL10]. There are several reasons for this success. First, it is very simple to implement, understand and use (especially by industry, software engineers, and generally all people that are not pure researchers but customers for our results and tools). Second, it requires little or no extra modeling or specification effort, but simply an operational model of the system that can be simulated and checked against properties. Third, the use of Statistics allows to approximate undecidable problems. Finally, it is possible to easily distribute SMC [BDLLMP12].
Why do we use Statistical Model Checking?
In a recent work [BDLLMPW11], we used the model of Priced Timed Automata (PTA), that are timed systems in which clocks may have different rates (even potentially negative) in different locations. Such automata are as expressive as linear hybrid automata or priced timed automata, but the addition of features such as input and output modalities allow us to specify complex problems in an elegant manner. Unfortunately most of such problems are either undecidable or too complex to be solved with classical model checking approaches (state-space explosion). Our solution:
- We define a stochastic semantic for CSTAs. This semantic is natural as it gives a stochastic meaning to timed behaviors. Moreover, it is preserved by composition.
- We apply SMC on the resulting stochastic timed system.
- Why is this different from Classical Uppaal?
There are two major differences with classical Uppaal: 1. the user interface allows to specify probability distributions that drive the timed behaviors, and 2. The engine offers a statistical model checking support capable of a) computing an estimate of a probability, b) compare a probability with a value, and c) compare two probabilities without computing them. Our engine relies on powerful results coming from the statistics such as sequential hypothesis testing, or Monte Carlo simulation.
Why are we better than other toolsets?
Classical SMC model checkers [You05a, SVA05b, KZHHJ09] are either capable of computing an estimate of the probability or test whether this probability is greater or equal to some value. All those implementations are unable to handle timed systems. Moreover, contrary to those implementations, our tool also implements those tests that can compare two probabilities without computing them. Finally, contrary to other SMC-based tools, the Uppaal extension comes with a wide range of functionalities that allows the user to visualize the results on the form of probability distributions, evolution of the number of runs with timed bounds, computation of expected values, … There are other very rich framework for specifying stochastic timed systems. An example of such framework is the MoDeST [BDArHK04] toolset. Here, however, general hybrid variables are not considered and parallel composition do not yield fully stochastic models. For the notion of probabilistic hybrid systems considered in [HSCC11] the choice of time is resolved non-deterministically rather than stochastically as in our case and as required by SMC.
References
- [BDLLMP12] Peter Bulychev, Alexandre David, Kim G. Larsen, Axel Legay, Marius Mikučionis, and Danny Bøgsted Poulsen. Checking & Distributing Statistical Model Checking. 4th NASA Formal Methods Symposium, 2012, pages 449-463, LNCS 7226, Springer.
- [JCLLPZ09] Sumit Kumar Jha, Edmund M. Clarke, Christopher James Langmead, Axel Legay, André Platzer, and Paolo Zuliani. A Bayesian Approach to Model Checking Biological Systems. In Proceedings of CMSB, pages 218-234, 2009, LNCS 5688, Springer.
- [CFLHJL08] Edmund M. Clarke, James R. Faeder, Christopher James Langmead, Leonard A. Harris, Sumit Kumar Jha, and Axel Legay. Statistical Model Checking in BioLab: Applications to the Automated Analysis of T-Cell Receptor Signaling Pathway. In Proceedings of CMSB, pages 231-250, 2008, LNCS, Springer.
- [You05a] H. L. S. Younes. Verification and Planning for Stochastic Processes with Asynchronous Events. Ph.D., Carnegie Mellon, 2005.
- [BBBCDL10] A. Basu, S. Bensalem, M. Bozga, B. Caillaud, B. Delahaye, and A. Legay. Statistical Abstraction and Model-Checking of Large Heterogeneous Systems. In Proceedings of FORTE, pages 32-46, 2010, LNCS 6117, Springer.
- [BDLLMPW11] Peter Bulychev, Alexandre David, Kim Guldstrand Larsen, Axel Legay, Marius Mikučionis, Danny Bøgsted Poulsen, and Zheng Wang. Statistical Model Checking for Priced Timed Automata. pdf.
- [SVA05b] K. Sen, M. Viswanathan, and G. A. Agha. VESTA: A Statistical Model-checker and Analyzer for Probabilistic Systems. In Proceedings of QEST 2005, pages 251-252. IEEE Computer Society.
- [KZHHJ09] J-Pieter Katoen, I. S. Zapreev, E. Moritz Hahn, H. Hermanns, and D. N. Jansen. The Ins and Outs of the Probabilistic Model Checker MRMC. In Proceedings of QUEST 2009, pages 167-176. IEEE Computer Society.
- [BDArHK04] H. Bohnenkamp, P.R. D’Argenio, H. Hermanns, and J.-P. Katoen. MoDeST: A compositional modeling formalism for real-time and stochastic systems. Technical report CTITT, 04-46, University of Twente, 2004.
- [HSCC11] Tino Teige, Andreas Eggers, and Martin Fränzle. Constraint-Based Analysis of Concurrent Probabilistic Hybrid Systems: An Application to Networked Automation Systems. In Nonlinear Analysis: Hybrid Systems, 2011.
Uppaal Stratego
Uppaal combines various analysis techniques from different Uppaal branches and focuses on strategies. In particular Uppaal Stratego facilitates generation, optimization, comparison as well as consequence and performance exploration of strategies for stochastic priced timed games in a user-friendly manner. The tool allows for efficient and flexible “strategy-space” exploration before adaptation in a final implementation by maintaining strategies as first class objects in the model-checking query language.
Concepts
A game is a mathematical model of a system consisting of several players (processes) which have independent objectives, often they are competing and sometimes opposing and even conflicting. To win a game the player needs to achieve the objective (goal). The simplest game consists of two players. Sometimes the game is symmetric (e.g. for reasons of fairness) where starting positions and objectives of the players are equivalent, but in general it does not need to be symmetric and most often it is not. Solving a game means finding a winning strategy leading to the goal or proving that the goal is not achievable. Games are interesting because game modeling is relatively easy (easier than proving theorems) and many mathematical proofs can be reduced to solving a game, therefore game solving tools help automate proving properties about a rich set of systems. Moreover, its diagnostic artefacts (strategies) can be used to generate controller algorithms, therefore effectively achieving correct-by-design controller is.
A strategy is a prescription of one player’s actions (transitions) for any possible situation (system state) eventually leading to achieving the player’s goal. The winning strategy does not always exists. Deterministic strategy specifies a single action per state and non-deterministic strategy may specify several alternatives. Fully permissive strategy specifies all alternative actions leading to the goal.
Uppaal timed game is a two-player game specified by a network of timed automata with two types of edges: solid and dashed, corresponding to the player- and opponent-chosen transitions. Uppaal TIGA uses symbolic techniques to solve timed games with dense time.
A stochastic timed game is a probabilistic extension to a timed game.
A stochastic priced timed game is a further extension with continuous price expressions which allow estimating the distribution of cost in a timed game.
Overview
Below is an overview of various models and strategies and their relations in Uppaal Stratego, where solid arrows indicate transformation and computation and dashed arrows indicate reuse of the objects:

The top layer is dedicated to symbolic methods, such as solving a timed game G by computing a strategy σ, which can already be achieved by Uppaal TIGA. The novelty here is that the newly computed strategy σ is stored in the memory and the model G can repeatedly be evaluated under the σ strategy using queries applicable to (stochastic) timed automata G|σ.
The bottom layer is dedicated to simulation-based methods, such as statistical model checking and learning-based synthesis of extended stochastic models. The stochastic extensions are similar to the ones introduced in Uppaal SMC except that the continuous dynamics is limited to price variable derivatives, whereas the price variable itself cannot be constrained (similar to cost variable in Uppaal CORA, except there can be many price variables). The stochastic priced timed game P contains probabilistic and priced extensions, but its behavior is compatible with the original timed game in a sense that probabilistic transitions can be treated as non-deterministic and price variables act only as monitors and thus can be ignored in a timed game setting. Therefore the model can be described in one coherent document as a stochastic priced timed game P and internally converted into a timed game G on demand while preserving the syntactic structure.
Some of the strategies σ, notably the most permissive kind, from timed game G describe a union of all possible strategies and thus contain multiple (non-determistic) options and thus these options can be price-optimized by synthesizing another strategy σ° on a stochastic priced timed game P which shares the same structure as G, thus effectively solving a stochastic priced timed game.
Similar to the above layer, the optimized strategies σ° can be further examined by (statistical) model checking P under σ°.
COSHY
Uppaal COSHY extends the Uppaal query langauge with the approximate control query which can synthesize safety strategies for a very general class of systems. This includes stochastic behaviour, continuous state-spaces and hybrid dynamics.
The query treats the (continuous) system as a (discretized) abstract game, approximating the behaviour of the game by sampling the real behaviour of the system. The result is a winning strategy for this game, which approximates a safety strategy for the system.
The safety strategies produced by approximate-control queries can permit several actions in the same state. As such, it is possible to use learning queries under the restrictions of a safety strategy. This enables the training of safe and near-optimal strategies.
The prototype can be downloaded from Download Other section.
Tiga
Uppaal TIGA (Fig. 1) is an extension of Uppaal [BDL04] and it implements the first efficient on-the-fly algorithm for solving games based on timed game automata with respect to reachability and safety properties. Though timed games for long have been known to be decidable there has until now been a lack of efficient and truly on-the-fly algorithms for their analysis. The algorithm we propose [CDFLL05] is a symbolic extension of the on-the-fly algorithm suggested by Liu & Smolka [LS98] for linear-time model-checking of finite-state systems. Being on-the-fly, the symbolic algorithm may terminate long before having explored the entire state-space. Also the individual steps of the algorithm are carried out efficiently by the use of so-called zones as the underlying data structure. Our tool implements various optimizations of the basic symbolic algorithm, as well as methods for obtaining time-optimal winning strategies (for reachability games).

References
- [BDL04] Gerd Behrmann, Alexandre David, and Kim G. Larsen. A Tutorial on Uppaal. LNCS 3185. Springer-Verlag 2004, pp 200-236.
- [CDFLL05] Franck Cassez, Alexandre David, Emmanuel Fleury, Kim G. Larsen, and Didier Lime. Efficient On-the-fly Algorithms for the Analysis of Timed Games. LNCS 3653. Springer-Verlag 2005, pp 66-80.
- [LS98] Xinxin Liu and Scott A. Smolka. Simple Linear-Time Algorithm for Minimal Fixed Points. LNCS 1443. Springer-Verlag 1998, pp 53-66.
Ecdar
ECDAR is a tool implementing the timed interface theory of DLLNW10. Its architecture reuses parts of Uppaal. The tool itself is the fruit of the collaboration between Aalborg University, INRIA (Axel Legay), and ITU (Andrzej Wąsowski).
The input language is timed I/O automata and is defined using, respectively, the modalities controllable and uncontrollable to define, respectively, inputs and outputs. ECDAR treats timed game automata as timed I/O automata and opens the way to incremental design and compositional reasoning.
The tool is designed to check incrementally refinement between specifications. As shown in Fig. 1, it is possible to combine different timed I/O automata with the composition or conjunction operators and check if the combined specification refines another specification (that can be defined with such operators as well).

Reference
- [DLLNW10] Alexandre David, Kim.G. Larsen, Axel Legay, Ulrik Nyman, and Andrzej Wąsowski. Timed I/O automata: a complete specification theory for real-time systems. The 13th ACM international conference on Hybrid systems: computation and control (HSCC) 2010.
CORA
Uppaal CORA is a branch of Uppaal for Cost Optimal Reachability Analysis developed by the Uppaal team as part of the VHS and AMETIST projects. Whereas Uppaal uses timed automata as its modelling language, Uppaal CORA uses linearly priced timed automata (LPTA). Given an LPTA model, Uppaal CORA finds the optimal paths to a state satisfying some goal conditions. Optimal here means the path with the lowest accumulated cost.
Uppaal CORA provides a number of extensions to the modelling language of Uppaal, that allows the user to convey additional insight about the model to the tool, which in turn can improve the performance of Uppaal CORA. In particular, it is possible to annotate the model with an estimate of the remaining cost for reaching a state satisfying the goal conditions. This can significantly reduce the time required for finding a good or an optimal solution.
About the Language
Uppaal CORA uses the LPTA modelling languages. “So what is an LPTA?”, you ask. Let us start with a timed automaton. A timed automaton is basically a finite state machine extended with a set of non-negative real valued variables called clocks. These variables are incremented synchronously with the passage of time. E.g. if 2.3 time units pass, then all clocks are incremented by 2.3. It is important to notice that the domain of clocks is the non-negative reals, thus the state space of a timed automaton is infinite. The edges of the timed automaton are annotated with guards and updates. Guards are conditions over the clocks; the edge is enabled if and only if the guard is satisfied. Updates are assignments that set the clock to a new value whenever the edge is taken. Finally, the vertices (which are called locations in timed automata) are labelled with invariants. Invariants are conditions that must be satisfied whenever the automaton is in that location (it is important to notice that invariants are not a way of checking whether the conditions are satisfied; invariants are satisfied by definition of a timed automaton – states where the invariant does not hold do not exist). The language used by Uppaal is somewhat more powerful: It supports integer variables, records, constants, arrays, parallel composition of several timed automata (which might synchronize via channels), arithmetic expressions and even functions with loops and conditional statements. If you are new to timed automata and Uppaal, we recommend reading the Uppaal tutorial.
An LPTA is a timed automaton that is extended with one addition variable: The cost. This is a monotonically increasing variable over the non-negative reals. Initially, it is zero. It might be incremented on the edges as part of the update (impulse cost). It can also increment with the passage of time with a specified rate. E.g. if the rate is 3 and 2.3 time units pass, then the cost is incremented with 6.9. The cost cannot be tested upon in any guard or invariants, so it does not influence the behaviour of the system – this is a very important restriction, as otherwise model checking of LPTA would become undecidable.
About AMETIST
Citing the AMETIST web-page:
The main objective of the AMETIST project was to develop a powerful modelling methodology supported by efficient computerized problem-solving tools for the modelling and analysis of complex, distributed real-time systems. In particular, the project addressed problems in connection with time-dependent behaviour and dynamic resource allocation. Problems of this type are manifested under different names in application domains such as manufacturing, transport, communication networks, real-time software and digital circuits. AMETIST intended to develop a unifying mathematical modelling framework for these phenomena based on the existing body of theory and tools for the so-called timed automata model, which has emerged as a very promising formalism for the modelling and analysis of real-time related phenomena. By doing so we moved the state-of-the-art to a new level of maturity.
TRON
Uppaal TRON is a testing tool [M10,LMNS05,LMN08,HLMNPS08], based on Uppaal engine, suited for black-box conformance testing of timed systems, mainly targeted for embedded software commonly found in various controllers. By online we mean that tests are derived, executed and checked simultaneously while maintaining the connection to the system in real-time.
Below are a screenshot of smart-lamp controller Java applet demo and automatically generated signal flow diagram of the system model:


Highlights
- Performs conformance testing: the tool checks whether the timed runs of the system under test (SUT) are specified in the system model (timed trace inclusion) and no illegal (unexpected, unspecified) timed behavior is observed.
- The emphasis is on testing the timed and functional properties. Time is considered continuous, (input/output) events can happen at any real-valued moment in time, but deadlines are constrained by integers (rationals). Test data generation is also possible, but (today) data types and value selection are limited by modeling language.
- The specification is an Uppaal timed automata network partitioned into a model of the system and a model of system’s environment assumptions. The model can be non-deterministic, allowing reasonable freedom for system implementations, modeling possible/tolerable time drifts, soft time deadlines.
- Test primitives are generated directly from the model, executed and the system responses checked at the same time, online (on-the-fly) while connected to the SUT, thus avoiding huge intermediate test suites.
- During testing the tool follows the environment model which can have various purposes:
- fully permissive environment model allows to test full conformance;
- a specific environment minimizes the testing effort for realistic level of conformance;
- environment model as use cases guide through functionality of a particular interest;
- environment model as pre-recorded test runs used to re-execute tests for debugging or regression testing.
- Uppaal model-checking engine allows efficient and fast timed automata model exploration.
- The choices of inputs and time delays are randomized.
- In general, testing the real-time conformance is undecidable, but under digitization assumptions it is shown to be sound and complete in a limit.
Setup
The system under test is attached to Uppaal TRON via a test-adapter (an SUT specific software layer) and considered as a black-box since its state cannot be directly observed; only communication events via input/output channels. The user supplies Uppaal TRON with the closed timed automata network of SUT model in parallel composition together with assumptions on environment.
The explicit environment model is an important feature: it can be used to generate test events only that are realistic it the operating environment. It may also be fully-permissible, meaning that the environment (testing tool in this case) can offer any input at any moment and accept any output at any moment. Finally it can be used to guide the test (which is randomized) to produce particularly interesting behaviors.
Further technical details are documented in Uppaal TRON User Manual.
References
- [M10] Marius Mikučionis. Online Testing of Real-Time Systems. Ph.D. thesis. Aalborg University, June, 2010. [pdf]
- [HLMNPS] Anders Hessel, Kim G. Larsen, Marius Mikučionis, Brian Nielsen, Paul Pettersson and Arne Skou. Testing Real-Time Systems Using UPPAAL. Formal Methods and Testing. Springer Berlin / Heidelberg. April 13, 2008. [bib,pdf]
- [LMN08] Online Testing of Real-time Systems Using Uppaal. Kim G. Larsen, Marius Mikučionis, Brian Nielsen. Formal Approaches to Testing of Software. Linz, Austria. September 21, 2004. [bib,pdf]
- [LMNS05] Kim G. Larsen, Marius Mikučionis, Brian Nielsen, Arne Skou. Testing Real-time Embedded Software using Uppaal-TRON - An Industrial Case Study. The 5th ACM International Conference on Embedded Software. Jersey City, NJ, USA. September 18-22, 2005. [bib,pdf,models]