UPPAAL Stratego Examples and Use Cases
Traffic Dilema
Suppose we need to travel to Sidney from Aalborg as soon as possible but we are not sure which mode of transport is the fastest: a bike, a car or a train. Each of them have different speeds and risks depending on traffic conditions. Below is a stochastic timed automaton capturing trip possibilities:
We start in the location Aalborg on the left, pack our things and leave within 2 minutes. Then we can choose/control our prefered mode of travel:
- Bike is relatively slow but it is the most predictable option which takes to Sydney in between 42 and 45 minutes and thus depends very little on uncontrollable traffic conditions.
- Car has a possibility of an Easy and fast trip in 20 minutes if traffic permits (probability weight 10 yields likelyhood of 10/11), but there is a risk of 1 in 11 to get stuck in Heavy traffic and thus the trip could be prolonged up to 140 minutes.
- Train have periodic schedules and thus may have a waiting time up to 6 minutes and it is quite likely (10 out of 11) that we will board the train successfully and spend up to 35 minutes in location Go before reaching Sydney. There is also a small risk (1 out of 11) that the train is canceled and we end up in Wait, where we would have to decide either to switch to another train or GoBack home and in Aalborg make a decision again.
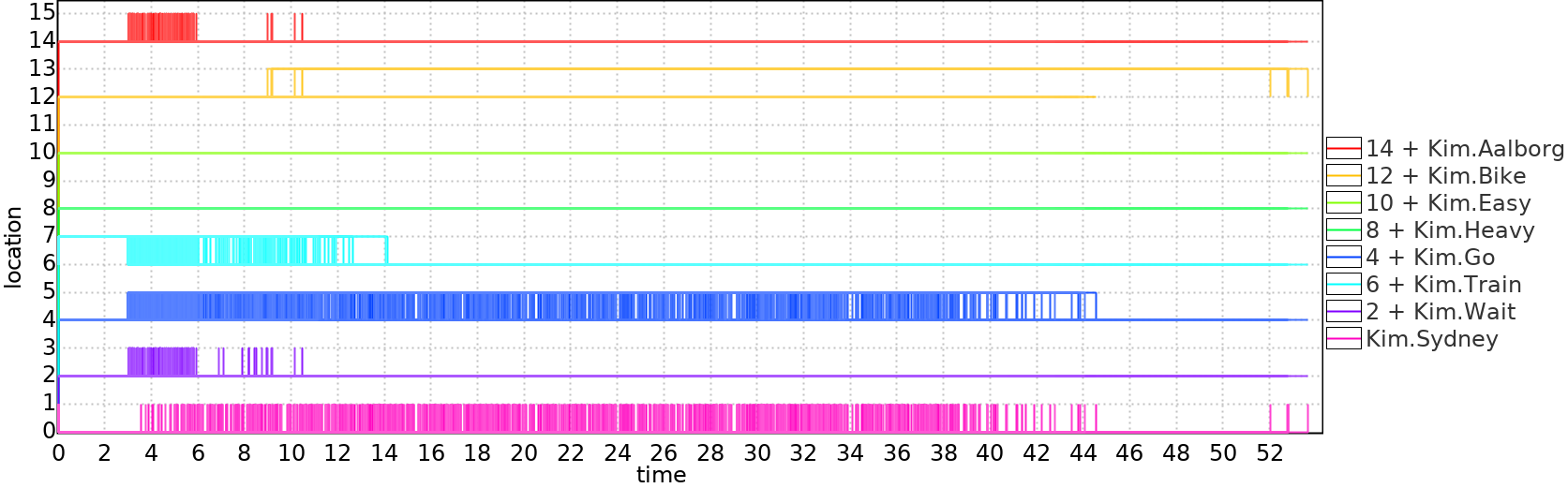
Given our model, we can inspect sample trip trajectories via SMC simulate query where the locations are encoded as different levels:
simulate 1 [<=100] {
Kim.Aalborg + 2*Kim.Bike + 4*Kim.Easy + 6*Kim.Heavy +
8*Kim.Train + 10*Kim.Go + 12*Kim.Wait + 14*Kim.Sydney }
Below are two sample trajectories computed by Uppaal Stratego:
| Normal train trip in 20 minutes: | Train and then bike in 50 minutes: |
|---|---|
|
|
|
The following queries and resulting plot show where and when the time is being spent:
simulate 100 [<=100] {
14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
6+Kim.Train, 4+Kim.Go, 2+Kim.Wait, Kim.Sydney
}
Pr[<=60](<> Kim.Sydney) // probability of reaching Sydney within 60 minutes is about 0.97 (not certain, thus not safe)
E[<=200 ; 500] (max: trip) // mean trip is about 28 minutes
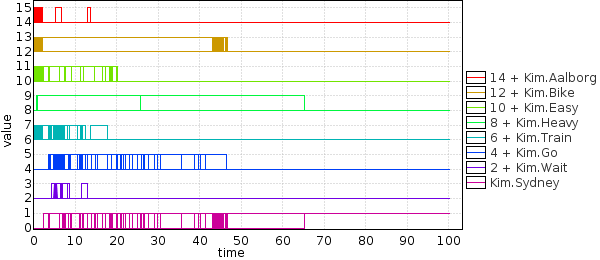
Generate and evaluate a safe strategy to get to Sydney within 60 minutes:
strategy GoSafe = control: A<> Kim.Sydney && time<=60
simulate 100 [<=100] {
14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
6+Kim.Train, 4+Kim.Go, 2+Kim.Wait, Kim.Sydney
} under GoSafe
A<> (Kim.Sydney && time<=60) under GoSafe // satisfied: using GoSafe we certainly reach Sydney within 60 minutes
E[<=200; 500] (max: trip) under GoSafe // mean trip time of GoSafe is about 33 minutes
The plot shows that most of the time is spent in Bike and Sydney and some in Train, therefore Bike is the sure way to reach Sydney but we can also risk catching a train within 10 minutes (if train does not come, we go back to Bike option).
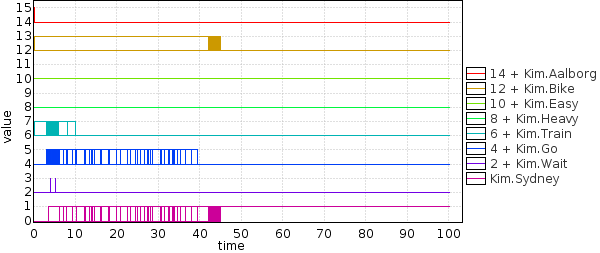
Learn fast strategy by minimizing the time to get to Sydney:
strategy GoFast = minE (trip) [<=200] : <> Kim.Sydney
simulate 100 [<=100] {
14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
6+Kim.Train, 4+Kim.Go, 2+Kim.Wait, Kim.Sydney
} under GoFast
Pr[<=60](<> Kim.Sydney) under GoFast // probability is about 0.94 (rushing is risky!)
E[<=200; 500] (max: trip) under GoFast // mean trip time is 15.4 minutes (almost 2x faster than no strategy)
The plot shows that most of the time is spent in Easy and Heavy and then Sydney, therefore Car is the fastest choice on average but we can get stuck in Heavy traffic and be late.
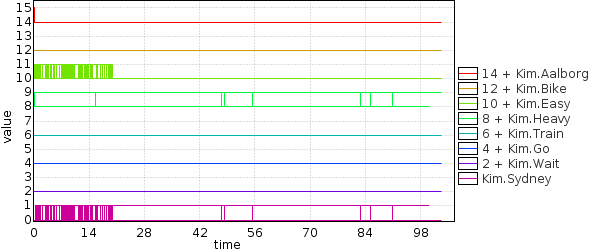
In order to get safe and fast strategy we optimize the GoSafe by minimizing the trip time to get to Sydney:
strategy GoFastSafe = minE (trip) [<=200] : <> Kim.Sydney under GoSafe
simulate 100 [<=100] {
14+Kim.Aalborg, 12+Kim.Bike, 10+Kim.Easy, 8+Kim.Heavy,
6+Kim.Train, 4+Kim.Go, 2+Kim.Wait, Kim.Sydney
} under GoFastSafe
Pr[<=60](<> Kim.Sydney) under GoFastSafe // probability is >0.99 (we could not find a counter-example)
E[<=200 ; 500] (max: trip) under GoFastSafe // mean trip time is 22.4 minutes (faster than GoSafe but not as fast than GoFast)
The result shows that Train is the safe and fast option, but a few times one may need to go back and pick a bike.
The model and queries can be downloaded here: traffic.xml.
A walkthrough video presented at ATVA 2014: ATVA14-walkthrough.wmv.
Newspaper and Travel
Model: newspaper.xml
Safe and Optimal Cruise Control
This example is dedicated to Ernst-Rüdiger Olderog [LMT15]. It demonstrates the usage of symbolic techniques in synthesizing a safe discrete controller for continuous dynamics and then optimizing the control for maximum progress by using statistical techniques — all within a single integrated tool Uppaal Stratego.
The goal of cruise control is to maintain steady speed of a vehicle. As roads are becoming more congested, an adaptive cruise control would also maintain a safe distance to vehicles ahead. Picture below captures a setup with our Ego car and a car in Front.
Ego is equiped with a distance sensor. The distance changes dynamically based on a relative speed between cars and each car controls its speed by acceleration or breaking. The goal is to synthesize a control strategy whether to accelerate, maintain speed, break or even move backwards based on measured relative distance.
Our proposed solution is to model the system as a Stochastic Priced Timed Game, abstract away the stochastic and continuous dynamics, solve the Timed Game with a safety goal (when Ego should accelerate or break but maintain minimal safe distance despite what Front may choose to do), then take the safe Ego strategy back to the original Stochastic Priced setup and optimize the safe controller strategy into fast one by using learning techniques.
Modeling
First we model the controllable options of such a system, namely the actions of car Ego of picking its acceleration values via solid edges:
Front car can also exercise the same actions, but for us its transitions are not controllable (dashed edges). In addition Front may go beyond the reach of Ego’s distance sensor (Faraway location):
We introduce a scheduler to limit the decision taking for both cars to once per second. The scheduler dictates that Ego should make its choice first without the knowledge of what Front’s choice, then Front may choose its acceleration (may turn against Ego’s choice) and after one second the discrete approximation of velocities and distance is calculated:
The approximate integer distance is calculated based on averages using the function below:
int distance; // approximated distance between cars
int velocityEgo, velocityFront; // approximated velocities
int accelerationEgo, accelerationFront; // discrete acceleration
void _updateDiscrete()_
{
int oldVel, newVel;
oldVel = velocityFront - velocityEgo;
velocityEgo = velocityEgo + accelerationEgo;
velocityFront = velocityFront + accelerationFront;
newVel = velocityFront - velocityEgo;
if (distance > maxSensorDistance) {
distance = maxSensorDistance + 1;
} else {
distance += (oldVel + newVel)/2;
}
}
The actual dynamics of continuous distance and velocities is specified by ordinary differential equations over “hybrid clocks” as an invariant expression:
hybrid clock rVelocityEgo, rVelocityFront; // continuous "real" velocities hybrid clock rDistance; // continuous "real" distance between cars hybrid clock D; // "cost" to be minimized: integral over distance double _distanceRate_(double velFront, double velEgo, double dist) { **if** (dist > maxSensorDistance) **return** 0.0; **else** **return** velFront - velEgo; }
The hybrid clocks here are special: they do not influence the behavior of the model but rather monitor the “cost” of a simulation run, consequently they are abstracted away under symbolic model checking queries and enabled in statistical queries. Likewise, the stochastic features become plain non-deterministic under symbolic model checking queries. The RESET location provides special hint for statistical learning (the syntax is going to change in the future): the looping edge resets the variables which should not influence the strategy. In this case all variables are ignored as noise except the process locations.
We validate the discrete approximation by inspecting both discrete and continuous trajectories. The plot shows that discrete variables have exactly the same values as continuous ones at integer time points:
simulate 1 [<=20] { rDistance, dist, rVelocityFront - rVelocityEgo, velocityFront - velocityEgo }
However the verification shows that the distance is not always safe:
A[] distance > 5 // FALSE - unsafe
Statistical model checking also shows that the probability of a crash is unacceptably high if Ego is driven randomly:
Pr[<=100] (<> distance <= 5) // [0.85, 0.86] (95% CI)
The resulting plot shows that the probability density is highest in the beginning and the cumulative probability is over 85% after 100 seconds:
Synthesis of Safe Strategy
Controller synthesis uses symbolic game-solving techniques where Front is an oponent/adversary, Ego is the controlable player and the goal is to maintain the safe distance. Like with other symbolic techniques the continuous dynamics is abstracted away with Uppaal Tiga query and the resulting strategy is stored under the name safe:
strategy safe = control: A[] dist > 5 // success
The synthesized strategy is validated by simulating model behavior with controller choices from safe strategy. The plot shows that the distance trajectories are above 5, i.e. model does not exhibit crashes anymore:
simulate 10 [<=100] rDistance under safe
Once we have the safe strategy we can also estimate the smallest safe distance for any relative velocity. The plot below is a result of many infimum queries (symbolic model checking) for each possible relative velocity value:
inf { velocityFront-velocityEgo == _v_ } : dist under safe
The plot shows that the distance has a quadratic dependency on velocity when the velocity is negative (i.e. Front is approaching towards Ego) and it is a bit more complicated when Front is moving away.
Maximizing Progress by Minimizing Distance
Previous section showed some properties of the safe strategy. Apart from being safe, the strategy also exhibits rich (non-deterministic) behavior saying that there are many ways to stay safe. An emediate remark follows that even though the distance is safe it can still be arbitrary large, i.e. Ego may choose to stay home or even drive backwards without any progress. In order to guarantee maximal progress Ego should follow Front as close as possible, i.e. the progress is maximized when the distance between the cars is minimized. A statistical learning query is used to select a particular controllable transition from a non-deterministic set of safe transitions with an objective to minimized the expected cumulative distance D after 100 seconds under safe strategy drive:
strategy safeFast = minE (D) [<=100]: <> time >= 100 under safe
The learned result is a another strategy stored under the name safeFast which can also be checked using statistical queries. For example, here is a number of random runs using safeFast strategy:
simulate 10 [<=100] rDistance under safeFast
Notice that the distance trajectories are no longer diverging. The efficiency of the strategies is contrasted by comparing probability distributions of distances, which shows that under the safeFast strategy the distance is reduced from 138 to 24 on average:
Pr[rDistance <= maxSensorDistance + 1] <> time >= 100 under safe
Pr[rDistance <= maxSensorDistance + 1] <> time >= 100 under safeFast
In fact the new strategy is so effective at following the front car that the number of possible relative velocities is restricted to a narrow range of [-4,4] (as oposed to [-22,30] under safe) as shown in histogram of distances over velocities:
The box plot also shows that the mean distances stay low and only rarely diverge beyond 70.
Uppaal Stratego model: cruise.xml